2 Vmbo K(GT) 10e editie

Vmbo K(GT): Deel 1, Hoofdstuk 4

Dit Hoofdstuk doen we aan het eind van jet jaar. We gaan door met Hoofdstuk 5.

Vmbo K(GT): Deel 1, Hoofdstuk 4

Dit Hoofdstuk doen we aan het eind van het jaar. We gaan door met Hoofdstuk 5.

Scan de QR code met je telefoon of tablet om het proefwerk te starten:

Of klik op de volgende link: test jezelf

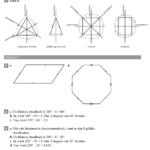
H 1.1 Namen van vlakke figuren: Werken met het stroomdiagram op de bladzijden 12 en 13.

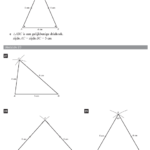
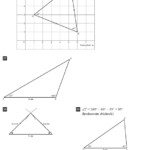
H 1.2 Driehoeken: Het gaat om de hoeken van een driehoek en een gestrekte hoek van 180°. Met de opgaven 9, 10 en 11 leer je dat dat de drie hoeken van een driehoek samen altijd 180° zijn. Er volgen allerlei hoekberekeningen in driehoeken, waarbij gebruik moet worden gemaakt van symmetrie, rechte hoeken en de eigenschap “som van de drie hoeken van een driehoek = 180°”.

H 1.3 Driehoeken tekenen: In deze paragraaf ga je driehoeken tekenen. Je leert eerst een schets te maken omdat je daarmee een stappenplan kan maken. Op bladzijde 22 staan alle mogelijkheden bij elkaar.

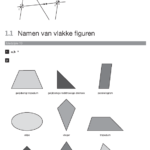
H 1.4 Vierhoeken: Je onderzoekt de eigenschappen van vierhoeken: vouwsymmetrisch of niet, draaisymmetrisch of niet. Het invullen van de tabel in opgave 64 dient nauwkeurig te gebeuren.

H 1.5 Hoeken berekenen in een vierhoek: Met overstaande hoeken en schuifsymmetrie wordt gekeken naar de hoeken in een parallellogram. Overstaande hoeken is ook een begrip dat gebruikt wordt. Er volgen nog hoekberekeningen in diverse vierhoeken. De vier hoeken van een vierkant zijn samen 360° moet je ook weten. Het berekenen van de hoeken is een puzzelachtig gebeuren.

H 2.1 Oplossen met grafieken: Het draait de hele paragraaf om het vinden van het snijpunt van twee grafieken en de betekenis van dat snijpunt.  Belangrijkste is dat het snijpunt wordt herkend als oplossing op de gestelde vraag.

H 2.2 Oplossen met inklemmen: De paragraaf begint met eenvoudige vergelijkingen die door jou op eenvoudige wijze zullen worden opgelost. Het gaat er nu om een getal te kiezen zodanig dat de vergelijking klopt: inklemmen. Na een paar keer oefenen gaat het inklemmen de meeste vlot af. Het opschrijven is een probleem: je bent vaak fanatiek met de rekenmachine in de weer om de oplossing te vinden en vergeet dan bij te houden wat je gedaan hebt. Een aantal mogelijkheden om te noteren: zie het voorbeeld op bladzijde 65.

H 2.3 De balansmethode: In deze paragraaf lossen we vergelijkingen van het type  2a  +  4  =  6 op met een balans. Eerst met tekeningen daarna wordt het moeilijker. Je krijgt een stappenplan. We beginnen met vergelijkingen met positieve getallen en daarna ook met negatieve getallen.

H 2.4 Uitgebreide balansmethode: We gaan vergelijkingen oplossen waarin aan beide kanten een variabele voorkomt. Het stappenplan wordt wat uitgebreid (rechts geen variabele).

H 3.1 Kwadraten en wortels: In deze eerste paragraaf oefen je met kwadraten en wortels. Als het goed is ken je de eenvoudige kwadraten nog uit het hoofd. We besteden aandacht aan wortels van decimale getallen. Uiteraard speelt de rekenmachine een belangrijke rol.

H 3.2 Machten: Van een kwadraat naar een macht is een kleine stap en die maken we hier dan ook. Het is een klein onderwerpje. Voor het berekenen mag je de rekenmachine gebruiken.

H 3.3 Rechthoekige driehoek: In deze paragraaf aandacht voor het benoemen van de verschillende zijden in een rechthoekige driehoek. De langste zijde ligt altijd tegenover de rechte hoek. Voor de rechthoekszijden gebruiken we ook de benaming korte zijden. We gaan rechthoekige driehoeken zoeken in complexere figuren.

H 3.4 De stelling van Pythagoras: Bij een rechthoekige driehoek tekenen we vierkanten op alle drie de zijden. We gaan werken met een schema: de zijde die je berekent herken je aan het vraagteken. We berekenen zowel de langste zijde als een van de korte zijden. Als je eraan went om altijd eerst het schema neer te zetten en het daarna in te vullen zal dat zeker goed gaan.

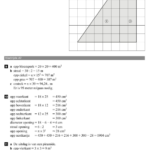
H 3.5 Pythagoras gebruiken: Allereerst het onderzoeken of een driehoek rechthoekig is. Dan verschillende problemen uit praktijksituaties die kunnen worden opgelost met de stelling van Pythagoras. Soms zijn hulplijnen nodig. Dan gaan we in roosters de lengte van een schuin lijnstuk berekenen. Ook hier moet je met hulplijnen eerst een rechthoekige driehoek maken. Tot slot bereken je de diagonalen op de zijvlakken van kubus en balk.

Vmbo K(GT): Deel 1, Hoofdstuk 4

Dit Hoofdstuk doen we aan het eind van het jaar. We gaan door met Hoofdstuk 5.

H 5.1 Oppervlakte driehoek: In de eerste opgaven en in de theorie op blz. 10 willen we laten zien dat de oppervlakte van een driehoek de helft is van de oppervlakte van de rechthoek die daar omheen past. We leren daarna de formule opp driehoek = ½ × zijde ×  bijbehorende hoogte aan. De oefenopgaven zijn bedoeld om te zorgen dat je bij een driehoek altijd op zoek gaan naar de hoogte en de zijde die loodrecht op elkaar staan.

H 5.2 Oppervlakte vierhoeken: Voor de oppervlakte van een parallellogram gebruiken we een vergelijkbare formule als voor de driehoek. Alleen is het dit keer niet de helft, zodat het wordt oppervlakte parallellogram = zijde × bijbehorende hoogte. In opgave 21 en 22 en de theorie op blz. 18 zie je waarom het zo is.

H 5.3 Omtrek en oppervlakte cirkel: In de eerste opgaven zie je dat de omtrek van een cirkel ongeveer 3 keer de middellijn is. In de theorie op blz. 27-28 leggen we uit dat het  3,1415926….is en introduceren we het getal pi (π). In de opgaven 55 en 56 maken we aannemelijk dat de oppervlakte van een cirkel = π × straal²  is.

H 5.4 Oppervlakte ruimtefiguren: In de theorie op bladzijde 31 laten we zien dat de oppervlakte van een ruimtefiguur de oppervlakte van de buitenkant is; dus gewoon de oppervlakte van alle vlakken bij elkaar optellen. Daarna bereken je de oppervlakte van een aantal bekende ruimtefiguren. Dat kan alleen als je het tot nu toe goed begrepen hebt en de formules goed kent.

6.1       Getallen: De onderwerpen zijn: waarde cijfers (bladzijde 52), grote getallen (bladzijde 53), delers (bladzijde 54), veelvouden (bladzijde 55), even en oneven (bladzijde 55) en product, quotiënt, som en verschil (bladzijde 56). Het zijn geen moeilijke begrippen, dus een klein aantal opgaven per onderwerp is voldoende.

6.2       Volgorde: De volgorde van bewerkingen in belangrijk. Het op een juiste manier berekeningen invoeren op de rekenmachine is minstens zo belangrijk. Op bladzijde 60 besteden we aandacht aan berekeningen met een deelstreep op de rekenmachine. De laatste theorie van de paragraaf behandelt het tegengestelde.

6.3       Formules met haakjes: En korte paragraaf waarin geoefend wordt met haakjes in formules.

6.4       Formules met een deelstreep: In paragraaf 2 hebben de leerlingen berekeningen met een deelstreep geoefend. In deze paragraaf wordt die vaardigheid toegepast in formules. Het herkennen van de getallen 52, 12 en 13 in de gegeven formules is nuttig. De context Lengte voorspellen komt uit de belevingswereld van de leerlingen. De getallen zijn realistisch.

6.5       Formules met kwadraten: In de rij met bouwwerken moet de regelmaat opvallen. Daarover gaan de opgaven 60 – 62. Daarna wat kwadratische formules en berekeningen daarmee. De gebruikte contexten, remweg, boog van een bal, valsnelheid, komen ook met regelmaat op het eindexamen voor. Het tekenen van de grafiek bij een kwadratische formule is heel wat complexer dan die bij een lineaire formule. We geven nog veel hulp. Ook laten we de symmetrieas zien. Dat kan veel onnodig rekenwerk voorkomen!

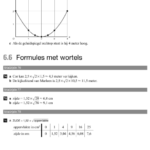
• Formules met wortels: Substitueren in een wortelformule en het tekenen van een grafiek bij een formule met een wortel is het onderwerp van deze paragraaf. Aandacht aan het tekenen van een vloeiende kromme.

• Periodieke verbanden: Bij een periodiek verband hoef je de formule niet te kennen. Het blijft bij het interpreteren van een gegeven periodieke grafiek. Van belang zijn de begrippen periode, maximum en minimum.

7.1       Diepte zien: Een kleine handleiding over hoe een kubus of een balk te tekenen. In feite wordt deze vaardigheid weinig gevraagd.

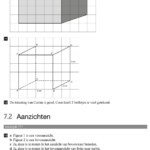
7.2       Aanzichten: In de techniek en de bouw wordt veel gewerkt met aanzichten. In deze paragraaf een kleine introductie daarop. Typisch voor de wiskunde zijn de bovenaanzichten van kubusbouwwerken met in de vierkantjes het aantal gestapelde blokjes, zoals op bladzijde 114. Zonder heel ingewikkeld te doen kan een je hiermee laten zien of je van een tweedimensionale tekening begrijpt welke driedimensionale figuur bedoeld wordt

7.3       Doorsneden: In deze paragraaf maak je kennis met doorsneden. Na enige oefening moet je doorsneden kunnen tekenen zonder het object ook echt door te snijden. Vaak is dat niet eens mogelijk zoals bij het colaflesje in opgave 24. De Extra opgave op bladzijde 116 zoek je naar afbeeldingen van doorsneden.

7.4       Inhoud berekenen: We gaan van allerlei ruimtefiguren de inhoud berekenen. Vanuit de bekende formule voor de balk komen we tot de formule inhoud = oppervlakte grondvlak × hoogte. Die is bruikbaar voor de balk, de kubus, het prisma en de cilinder. Het verschil zit in de oppervlakteberekening van het grondvlak, maar daar is in hoofdstuk 5 goed mee geoefend.

7.5       Inhoud piramide en kegel: In opgave 45 laten we zien dat een piramide drie keer past in een kubus of balk die daar precies omheen past. Zo maken we aannemelijk dat de inhoud van een piramide hetzelfde is als de inhoud van de kubus of balk x ⅓. We stellen daarna in de theorie op bladzijde 125-126 dat dat ook voor de kegel geldt.

8.1       Vergrotingsfactor: We beginnen met Google Maps. Dat is een van de vele programma’s op de computer waarmee je naar hartenlust kaarten kunt vergroten en verkleinen. Ook op de alomtegenwoordige smartphones en tablet zit zo’n functie. De leerlingen zijn daardoor erg vertrouwd met het groter en kleiner maken van afbeeldingen. Dan volgen een aantal opgaven waarin lenzen een rol spelen. Met een foto en zijn vergroting gaan we aan het rekenen in opgave 2. Je moet wel nauwkeurig meten. Van belang is de vraag hoeveel keer vergroot is en dan zo zijn we al bij de vergrotingsfactor. We kiezen voor de definitie
vergrotingsfactor =  lengte beeld  :  lengte origineel. Zo kunnen we ook naar verkleiningen. In de theorie op bladzijde 151 zien ze dat er dan een vergrotingsfactor kleiner dan 1 uitrolt. Tot slot nog wat vergrotingsopdrachten in Word.

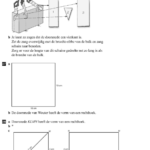
8.2       Gelijkvormige driehoeken: In deze paragraaf worden gelijkvormige driehoeken op de formele manier benaderd. In de Extra opgave op bladzijde 158 moet je een schets maken van een situatie en gelijkvormige driehoeken gebruiken om de hoogte van een boom te berekenen.

8.3       Oppervlakte en inhoud vergroten: Dat bij een vergroting de oppervlakte wordt vergroot met het kwadraat van de vergrotingsfactor is voor de meeste vrij helder. Dan is het nog een kleine stap naar de derde macht bij het vergroten van de inhoud. Toch is dat een lastig onderwerp, omdat de uitkomsten gevoelsmatig onwaarschijnlijk zijn.

8.4       Schaal: Bij plattegronden, maquettes en modellen hebben we te maken met een verkleining en een schaal, evenals bij (land)kaarten. Soms wordt een schaallijn gebruikt. We zien dat in atlassen en ook hier besteden we er aandacht aan. De paragraaf eindigt met het maken van een paar schaaltekeningen in opgave 71 en 72. Dit soort tekeningen nakijken met een antwoordenboekje is niet altijd een succes.